Calculation of smoking rates by dong/eup/myeon unit using small-area estimation in the Community Health Survey
Article information
INTRODUCTION
The Korean Community Health Survey (CHS), a community-based nationwide annual survey with the objective of providing important health indicators, is conducted through stratified cluster sampling and computer-assisted personal interviewing. Using the dong/eup/myeon administrative units (hereafter units) and residential structures (apartment or single house) as stratification variables, 900 adults (age≥19 years) per community health center district (hereafter district) are sampled and proportionally distributed across the units and according to residential structures, followed by selecting tong/ban/ri-level sample points via probability proportionate sampling based on the number of households. From each selected sample point, five households on average are selected by systematic sampling, and individual interviews are conducted with all adults in each household [1]. Although district-level health indicators are produced with a specific level of precision, there is an increasing demand for producing unit-level health indicators. However, the unit sample size varies considerably ranging between tens and several hundreds, and health indicators such as smoking rate for units with fewer than 30 samples produced using conventional statistical estimation methods cannot be used, owing to an exceedingly large sample variance of the estimates. This problem can be addressed by calculating unit-level statistics using a special estimation method such as small-area estimation [2]. This paper presents an optimized estimation method using Statistical Analysis System (SAS) codes.
Small-area estimation
Small-area estimation is an estimation method designed to produce statistics for small survey areas not included in the sample design for statistics and having unusable high-variance estimates owing to excessively small sample sizes, through supplementary use of surrounding area survey information, auxiliary information from other sources, or statistical model of the population [3,4].
Given that the sample design for the Community Health Service is intended to produce district-level health indicators, small-area estimation is needed for producing reliable unit-level health indicators. The following describes the small-area estimation methods for producing unit-level health indicators [5].
Direct estimator
A direct estimator uses only data obtained from the units concerned to produce unit-level health indicators. Each observation included in the survey data sets is given a weight item by item; the sample design-based direct estimator and its variance can be expressed by the following estimation equation, using weighted and observed values:
where ni is the sample size of unit i,
The variance of the estimator shown in Equation (1) can be obtained using Equation (2), as follows:
Where
Synthetic estimator
A synthetic estimator can yield more accurate unit-level estimates by using various auxiliary data, such as sex, age, and registered population, for each unit within a district [4,5]. After grouping the units into 2 to 3 homogeneous clusters, using their social environments and population ratios as clustering variables, under the assumption that the units of the same cluster might have similar sex-dependent/age-dependent health indicators, such as smoking rate, unit-level smoking rates can be calculated as follows, by combining smoking rates by sex and age group and by the number of people registered:
Where
The variance of the estimate shown in Equation (3) can be obtained using Equation (4):
where
While a synthetic estimator is potentially biased, the bias is considered negligible, given that the clustering of units within the same district ensures the sex/age category characteristics across units. If the bias exceeds a negligible level, attention must be paid to the clustering, because the equation for estimating the variance shown in Equation (4) tends to underestimate the estimation error of the estimator of Equation (3).
Composite estimator
Although the direct estimator shown in Equation (1) is unbiased, its estimates are not reliable, with unacceptably large standard error resulting from the small sample size, whereas the synthetic estimator shown in Equation (3) is biased. These problems can be addressed using a hybrid approach of obtaining more reliable estimates from the weighted average of the two estimators. The formula of weighted estimate average shown in Equations (1) and (3) is referred to as a composite estimator and can be calculated as follows:
where α is the weight that minimizes
While the optimal value of α is expected to be the one that minimizes the root mean square error of
Calculation of smoking rate using statistical analysis system
The following describes the calculation process of the unit-level smoking rates using the 2013 CHS data by applying small-area estimation to the calculation of smoking rates for the 22 dongs in Gangnam-gu, Seoul.
Direct estimator
The sample size distribution of the 22 dongs of Gangnam-gu included in the 2013 CHS shows that the dongs with the smallest and largest sample sizes are Gaepo 4- dong (n=24) and Yeoksam 1-dong (n=58). The smoking rates by dong were calculated using the direct estimators shown in Equation (1) and the variance estimation Equation (2) using SAS code as follows. The R-code program was presented in a previous study [6].
/*Generating the variables age groups and smoking/non-smoking from the Gangnam health center data*/ data abc.seoul_gangnam_data; set abc.chs13; length age_group $8.0 keep josa_year dong sm_a0100 sma_01z2 sma_03z2 age age_group sex wt; rename dong=eup/myeon/dong;;\ if 19<=age<=39 then age_group=”19-39 years”; if 40<=age<=59 then age_group=”40-59 year”; if 60<=age then age_group=”60 years and over”; ** Current smoking rate (refer to [7] for other survey item variables) ========================= Variable name: sm_a0100 (current smoking rate calculation variable) Analysis data variable name: sma_01z2(permanent smoking or not) sma_03z2(current smoking or not) ========================; if sma_01z2 = 1 then do; if sma_03z2 in (1,2) then sm_a0100=1; else if sma_03z2 = 3 then sm_a0100=0; end ; else if sma_01z2 = 2 then do; sm_a0100 = 0; end ; if bogun_cd=001; (Gangnam-gu health center code) run; /*Direct estimator and variance estimation of Gangnam-gu, Seoul*/ proc survey means data=abc.seoul_gangnam_data; var sm_a0100; (current smoking rate calculation variable) domain eup/myeon/dong; weight wt; (sample design weight) ods output Domain=abc.direct_estimator; run;
Synthetic estimator
To calculate the synthetic estimators of smoking rates by dong, the 22 dongs of Gangnam-gu were grouped into three clusters. After calculating the smoking rates of each cluster by sex and age group (19 to 39, 40 to 59, ≥60), the smoking rates and variances by dong were calculated using Equations (3) and (4), respectively, as follows:
① Calculation of the registered population ratios by sex and age group of 22 dongs as of the end of July 2013
② Grouping 22 dongs in three clusters using the k-means method, with the population ratio and smoking rate as clustering variables, and with a homogeneity check of the clustered groups against the registered population size and socioeconomic environment
/*Cluster analysis according to the smoking rates of population ratios by sex and age group in Gangnam-gu, Seoul as of 2013*/ /*Data retrieval*/ proc import out=abc.seoul_gangnam_cluster_ data datafile=”D: \2014_research_activities\sas_ lecture\seoul_gangnam-gu_cluster_data” datafile=dbms=excel replace; rage=”Seoul$” getnames=yes; mixed=no; scantext=yes; usedate=yes; scantime=yes; run; Imported data set is given Table 1. /*k-average clustering*/ proc fastclus data=abc.seoul_gangnam_cluster_data maxc=3 out=abc.seoul_gangnam_kcluster; var male_2013_19_39_years male_2013_40_59_years male_2013_60_over female_2013_19_39_years female_2013_40_59_years female_2013_60_over; id eup/myeon/dong; run; /*Export clusters to Excel*/ proc exprot data=abc.seoul_gangnam_kcluster OUTFILE= ”D: \2014research_activities\sas_ lecture\Seoul_gangnam-gu_cluster_analysis” label dbms=excel replace; run; /*Cluster correction*/ proc import out=abc.seoul_gangnam_rcluster datafile=”D:\2014research_activities\sas_ lecture\Seoul_gangnam-gu_corrected_clustering” dmbs=excel replace; rage=”seoul$” getnames=yes; mixed=no; scantext=yes; usedate=yes; scantime=yes; run;
③ Smoking rates of each cluster by sex and age group
/*Corrected cluster integration in data from Gangnam-gu, Seoul*/ proc sort data=abc.seoul_gangnam_data; by eup/ myeon/dong; run; proc sort data=abc.seoul_gangnam_rcluster; by eup/myeon/dong; run; data abc.seoul_gangnam_data2; merge abc.seoul_gangnam_data abc.seoul_gangnam_rcluster; by eup/myeon/dong; group1=corrected_cluster||”_”||sex||”_”||age_group; group1=compress(group1); run; proc print data=abc.seoul_gangnam_data2; run; The corrected data set is displayed in Table 2. /*Calculation of the estimated smoking rates of each cluster by sex and age group*/ proc surveymeans data=abc.seoul_gangnam_data2 mean; var sm_a0100; domain group1; weight wt; ods output Domain=abc.com_estimator_r; run; The results of calculation are contained in Table 3.
④ Calculation of synthetic estimates and variances of the smoking rates in 22 dongs
/*Preparation of the data for the cluster-level sex/age-dependent smoking rate estimation*/ /*Corrected cluster integration in data from Gangnam-gu, Seoul*/ proc sort data=abc.seoul_gangnam_data; by eup/myeon/dong; run; proc sort data=abc.seoul_gangnam_rcluster; by eup/myeon/dong; run; data abc.seoul_gangnam_data2; merge abc.seoul_gangnam_data abc.seoul_gangnam_rcluster; by eup/myeon/dong; group1=corrected cluster||”_”||sex||”_”||age_group; group1=compress(group1); run; /*Synthetic estimator for the 22 dongs in Gangnam-gu, Seoul*/ proc surveymeans data=abc.seoul_gangnam_com mean; domain eup/myeon/dong; var mean; weighted population; ods output domain=abc.seoul_gangnam_comestimator_mean; run; Synthetic estimates are displayed in Table 4. /*Variance estimation of the synthetic estimators for each dong*/ proc sort data=abc.seoul_gangnam_data2; by group1; run; data abc.seoul_gangnam_comvar; merge abc.seoul_gangnam_data2 abc.com_estimator_r; by group1; sum_wj_yj_rj=((wt*wt)*((sm_a0100-mean)*(sm_a0100-mean))); run; /*Total weights of the k-category within a cluster*/ proc surveymeans data=abc.seoul_gangnam_comvar; domain group1; var wt; ods output domain=abc.seoul_gangnam_comvar_1; run; /*Total for the intragroup k-category variance estimation*/ proc tabulate data=abc.seoul_gangnam_comvar; class group1; var sum_wj_yj_rj; table group1*sum_wj_yj_rj; ods output table=abc.seoul_gangnam_comvar_2; run; data abc.seoul_gangnam_comvar_data1; merge abc.seoul_gangnam_pop abc.seoul_gangnam_comvar_1 abc.seoul_gangnam_comvar_2; by group1; keep eup/myeon/dong cluster sex age-group population N Mean sum_wj_yj_rj_sum group1; run; Table 5 contains the generated data set. proc surveymeans data=abc.seoul_gangnam_comvar_data1 sum; domain eup/myeon/dong; var population; ods output domain=abc.seoul_gangnam_comvar_data2; run; proc sort data=abc.seoul_gangnam_comvar_data1; by eup/myeon/dong; run; proc sort data=abc.seoul_gangnam_comvar_data2; by eup/myeon/dong; run; /*Synthetic estimator variance estimation*/ data abc.seoul_gangnam_comvar_data; merge abc.seoul_gangnam_comvar_data1 abc.seoul_gangnam_comvar_data2; by eup/myeon/dong; drop varname varlabel stddev DomainLabel; Zjk=Population/Sum; Var=((Zjk*Zjk)/((N*(N-1))*(mean*mean)))*sum_wj_yj_rj_sum; run; Table 6 contains variance of syntyetic estimate. proc surveymeans data=abc.seoul_gangnam_comvar_data sum; domain eup/myeon/dong; var var; ods output domain=abc.seoul_gangnam_comvariance; run;
⑤ Data set generation by integrating the synthetic estimates and variance estimates for the smoking rates in all 22 dongs
/*Data integration of dong-level synthetic estimates and variance estimates*/ /*Synthetic estimator and variance*/ data abc.seoul_gangnam_estimator_com; merge abc.seoul_gangnam_comestimator_mean abc.seoul_gangnam_comvariance; by eup/myeon/dong; drop DomainLabel VarName stderr StdDev; rename mean=Y_s sum=var_Y_s; run;
Composite estimator
The dong-level direct and synthetic estimates of smoking rates are combined as weighted averages to calculate the composite estimates, thereby applying the following three methods for calculating weighted values.
First, αi for minimizing the mean square error of the composite estimator
The estimated value of the optimal weight αi(opt) is calculated as follows:
The weight minimizing the mean
The weight dependent on the sample size assigned to each small area is calculated as follows:
where N_i is the size of small area
After calculating the composite estimators of the dong-level smoking rates with each of the three types of weight presented above, an optimal estimation method is selected. The composite estimates are calculated in the following procedure.
① Data set generation integrating the direct estimates (Y_d) and synthetic estimates (Y_s) calculated for the 22 dongs
/Integration of direct and synthetic estimators (estimates and variance)*/ data abc.seoul_gangnam_estimators; merge abc.seoul_gangnam_estimator_direct abc.seoul_gangnam_estimator_com; by eup/myeon/dong; run; Table 7 contains the direct and synthetic estimates.
② Calculation of composite estimates using the first weight (Y_c1)
/*Composite estimator_1*/ data abc.seoul_gangnam_estimator_c1; set abc.seoul_gangnam_estimators; alpha1=Var_Y_s/(Var_Y_d+Var_Y_s); Y_c1=(alpha1*Y_d)+((1-alpha1)*Y_s); Var_Y_c1=((alpha1*alpha1)*Var_y_d)+(((1-alpha1)*(1-alpha1))*var_Y_s); sumvar_Ys_Yd=(var_Y_s+var_Y_d); run; /*Direct estimator variance by corrected cluster and direct estimator variance + composite estimator*/ proc surveymeans data=abc.seoul_gangnam_estimator_c1 sum; domain corrected cluster; var Var_Y_d; ods output domain=abc1; run; data abc1; set abc1; rename sum=sum1; run; proc surveymeans data=abc.seoul_gangnam_estimator_c1 sum; domain corrected cluster; var sumvar_Ys_Yd; ods output domain=abc2; run; data abc3; merge abc1 abc2; by corrected cluster; alpha2=1-(sum1/sum); keep corrected cluster alpha2; run; proc sort data=abc.seoul_gangnam_estimator_c1; by corrected cluster; run;
③ Calculation of composite estimates using the second weight (Y_c2)
/*Composite estimator_2*/ data abc.seoul_gangnam_estimator_c2; merge abc.seoul_gangnam_estimator_c1 abc3; by corrected cluster; Y_c2=(alpha2*Y_d)+((1-alpha2)*Y_s); Var_Y_c2=((alpha2*alpha2)*Var_y_d)+(((1-alpha2)*(1-alpha2))*var_Y_s); run; proc surveymeans data=abc.seoul_gangnam_pop sum; domain eup/myeon/dong; var population; ods output domain=abc4; run; proc surveymeans data=abc.seoul_gangnam_pop sum; domain corrected cluster; var population; ods output domain=abc5; run; proc surveymeans data=abc.seoul_gangnam_estimator_c2 sum; domain corrected cluster; var N; ods output domain=abc6; run; proc sort data=abc4; by eup/myeon/dong; run; data abc5; set abc5; rename Sum=cluster population; run; proc sort data=abc5; by corrected cluster; run; data abc6; set abc6; rename Sum=cluster sample size; run; proc sort data=abc6; by corrected cluster; run; proc sort data=abc.seoul_gangnam_estimator_c2; by eup/myeon/dong; run; data abc.seoul_gangnam_estimator_c3_1; m erge abc.seoul_gangnam_estimator_c2 abc4; by eup/myeon/dong; drop DomainLabel VarName VarLabel StdDev; rename sum=registered number of population; run; proc sort data=abc.seoul_gangnam_estimator_ c3_1; by corrected cluster; run; data abc.seoul_gangnam_estimator_c3_2; merge abc.seoul_gangnam_estimator_c3_1 abc5 abc6; by corrected cluster; drop DomainLabel VarName VarLabel StdDev; run;
④ Calculation of composite estimates using the third weight (Y_c3)
/*Composite estimator_3*/ data abc.seoul_gangnam_estimator_c3; set abc.seoul_gangnam_estimator_c3_2; hat_N_i=cluster population*(N/cluster sample size); if hat_N_i>=((2/3)*number of registered population) then alpha3=1 else alpha3=hat_N_i/((2/3)*number of registered population); Y_c3=(alpha3*Y_d)+((1-alpha3)*Y_s); Var_Y_c3=((alpha3*alpha3)*Var_y_d)+(((1-alpha3)*(1-alpha3))*var_Y_s); run;
⑤ Calculation of the composite estimates using the average weight of the first and third weights (Y_c4)
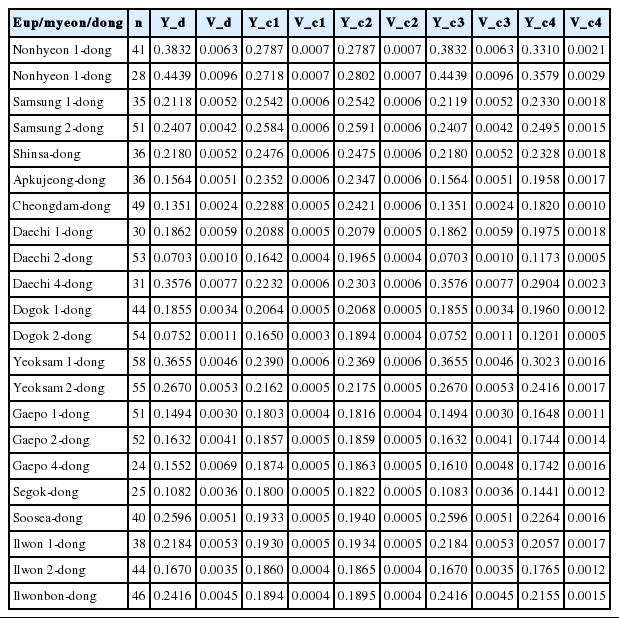
/*Composite estimator_4*/ data abc.seoul_gangnam_estimator_c4; set abc.seoul_gangnam_estimator_c3; alpha4=(alpha1+alpha3)/2 Y_c4=(alpha4*Y_d)+((1-alpha4)*Y_s); Var_Y_c4=((alpha4*alpha4)*Var_y_d)+(((1-alpha4)*(1-alpha4))*var_Y_s); run; /*Direct estimator_synthetic estimator_composite estimator*/ data abc.estimator_total; set abc.seoul_gangnam_estimator_c4; keep eup/myeon/dong Y_d Var_Y_d Y_s var_y_s alpha1 Y_c1 var_Y_c1 alpha3 Y_c3 var_y_c3 Y_c4 var_y_c4; run; proc print data=abc.estimator_total; run;
Table 8 outlines the results of calculating the current smoking rates of each of the 22 dongs applying the four types of composite estimates. While variances are found to be lower compared with direct estimates, the current smoking rate estimates vary widely depending on dong sample sizes, reflecting the estimate-stabilizing feature of composite estimation. Viewed from the aspect of reducing the variance of direct estimates and correcting the bias of synthetic estimates, the fourth composite estimator is considered most effective in stabilizing the dong-level estimates.
CONCLUSION
This paper explained the procedure for producing health indicators at dong/eup/myeon-level (smaller than the designed domain) from the CHS data with the aim of producing health indicators at the level of health center district (designed domain), by applying small-area estimation to an example case of numerical estimation. The calculation procedures were presented using SAS codes, a method that is expected to be useful in cases in which statistics for smaller or detailed areas are to be produced from a survey conducted with the objective of producing statistics at a larger domain level.
Acknowledgements
This work was supported by the Research Program funded by the Korea Centers for Disease Control and Prevention (fund code 2014-P33001-00).
Notes
The author has no conflicts of interest to declare for this study.
SUPPLEMENTARY MATERIAL
Supplementary material is available at http://www.e-epih.org/.